Az útvonalkereső célja, hogy tetszőleges térképen bármely két pont között visszaadja az egyik legrövidebb útvonalat. A* keresés esetén a térképnek az alábbi feltételeknek kell megfelelnie:
- Bármely pontjára lekérdezhető az adott pont összes közvetlen szomszédja és az oda eljutás költsége
- Bármely tetszőleges két pontjára tud adni egy alsó becslést a két pont távolságára, ezt hívjuk heurisztikának
Lényegében az alábbi interface-t kell, hogy megvalósítsa:
#include <vector>
class IMap
{
public:
typedef std::pair<int, float> Neighbour_t;
typedef std::vector<Neighbour_t> Neighbours_t;
virtual void GetNeighbours( int aNode, Neighbours_t& aNeighbours ) const = 0;
virtual float GetDistance( int aNodeFrom, int aNodeTo ) const = 0;
};
A node-ok most az egyszerűség kedvéért sima indexek (egy adott pont a térképen), illetve az int-float páros a node-költség párosok, vagyis a szomszédos pont indexe és az oda való eljutás költsége. Például ha egy országos vasút térképet képzelünk el, akkor az indexek az állomások sorszámozva, a szomszédok azon állomások, ahova egy megállót utazva jutunk el, a költség a megtett táv, és két állomás közötti távolság vagyis a heurisztika a köztük légvonalban mért távolság. Ideális körülményeket feltételezve, vagyis mindig megy mindenhova vonat, nincs költsége az átszállásnak és a vonat mindenhol ugyanolyan tempóval halad, vagyis egyforma költsége van bármely vonalon való utazásnak.
A keresés megkezdése előtt definiáljunk egy úgy nevezett open-list-et, ez azon pontok listája amiket a keresés során érintettünk. Ezen node-okhoz 3 érték tárolására lesz szükség, G, H és F, valamint a szülő node indexére, a pont ahonnan ide jutottunk. G a pontba való eljutás költsége a kezdőponttól, H a végpontig hátralévő becsült költség, vagyis a heurisztika, F pedig a két érték összege, vagyis a teljes út becsült költsége. Lesz ezen kívül egy closed-list-ünk, ebbe kerülnek azon pontok, melyek vizsgálatát már befejeztük.
struct sNode
{
float G;
float H;
float F;
int Parent;
};
#include <map>
#include <deque>
class AStar
{
private:
typedef std::map<int, sNode*> OpenList_t;
typedef std::map<int, const sNode*> ClosedList_t;
public:
typedef std::deque<int> Path_t;
private:
OpenList_t mOpenList;
ClosedList_t mClosedList;
const IMap& mMap;
private:
OpenList_t::iterator GetBestOpenNode();
void GeneratePath( int aNodeTo, Path_t& aPath ) const;
void Cleanup();
public:
AStar( const IMap& aMap );
bool FindPath( int aNodeFrom, int aNodeTo, Path_t& aPath );
};
Maga az algoritmus pedig:
- Rakjuk be a kezdőpontot az open list-be, 0 eddigi költséggel és a becsült hátralévővel
- Rakjuk át az open-list-ből a legkisebb becsült teljes költségűt a closed-list-be
- Ha ez a célpont, akkor kész vagyunk
- Ha nem volt már node az open-list-ben, akkor nem létezik útvonal
- Kérjük le az átrakott node összes szomszédját az oda való eljutás költségével együtt
- Vegyük az első (következő) kifejtett child node-ot, ha van, amúgy vissza a 2-es pontra
- Ha a kifejtett node már a closed-list-ben szerepel, akkor a 6-os ponttól folytassuk
- Az új node eddigi költsége az átrakott node eddigi költsége és az onnan az új node-ba való eljutás költségének összege lesz
- Ha az új node még nem szerepel az open listában, akkor vegyük fel oda és kérjük le a becsült hátralévő költséget, vagyis számoljunk heurisztikát a végpontra
- Ha szerepel az open-list-ben, akkor frissítsük be, amennyiben a számolt új költség kisebb mint az eddigi
- Amennyiben ez előző két pontban történt változás, számoljuk ki a becsült teljes költséget, ami az eddigi költség és a becsült hátralévő összege
- Menjünk vissza a 6-os pontra
Amennyiben az algoritmusunk talált útvonalat, a szülő node-okon végigmenve a kezdőpontig megkapjuk a teljes útvonalat fordított sorrendben. Ha esetleg nem találtunk volna utat, a closed-list-ből kikereshető a legkisebb H értékű node, ami a célponthoz legközelebbi pont, és ehhez is visszafejthető egy út.
Az algoritmus C++ megvalósítása:
AStar::AStar( const IMap& aMap )
: mMap( aMap )
{
}
AStar::OpenList_t::iterator AStar::GetBestOpenNode()
{
float BestF = FLT_MAX;
OpenList_t::iterator ItBestNode;
for( OpenList_t::iterator ItNode = mOpenList.begin();
ItNode != mOpenList.end(); ++ItNode )
{
const sNode* Node = ItNode->second;
if( Node->F < BestF )
{
ItBestNode = ItNode;
BestF = Node->F;
}
}
return ItBestNode;
}
void AStar::GeneratePath( int aNodeTo, Path_t& aPath ) const
{
do
{
aPath.push_front( aNodeTo );
const sNode* Node = mClosedList.find( aNodeTo )->second;
aNodeTo = Node->Parent;
}
while ( aNodeTo != -1 );
}
void AStar::Cleanup()
{
for( OpenList_t::const_iterator ItNode = mOpenList.begin();
ItNode != mOpenList.end(); ++ItNode )
{
const sNode* Node = ItNode->second;
delete Node;
}
mOpenList.clear();
for( ClosedList_t::const_iterator ItNode = mClosedList.begin();
ItNode != mClosedList.end(); ++ItNode )
{
const sNode* Node = ItNode->second;
delete Node;
}
mClosedList.clear();
}
bool AStar::FindPath( int aNodeFrom, int aNodeTo, Path_t& aPath )
{
sNode* OpenNode = new sNode;
OpenNode->G = 0;
OpenNode->H = mMap.GetDistance( aNodeFrom, aNodeTo );
OpenNode->F = OpenNode->G + OpenNode->H;
OpenNode->Parent = -1;
mOpenList[ aNodeFrom ] = OpenNode;
while( !mOpenList.empty() )
{
OpenList_t::iterator ItNode = GetBestOpenNode();
int NodeIndex = ItNode->first;
const sNode* Node = ItNode->second;
mOpenList.erase( ItNode );
mClosedList[ NodeIndex ] = Node;
if( NodeIndex == aNodeTo )
{
GeneratePath( aNodeTo, aPath );
Cleanup();
return true;
}
IMap::Neighbours_t Neighbours;
mMap.GetNeighbours( NodeIndex, Neighbours );
for( IMap::Neighbours_t::const_iterator ItNeighbour = Neighbours.begin();
ItNeighbour != Neighbours.end(); ++ItNeighbour )
{
int ChildNodeIndex = ItNeighbour->first;
if( mClosedList.find( ChildNodeIndex ) != mClosedList.end() )
{
continue;
}
sNode* ChildNode = NULL;
float NewG = Node->G + ItNeighbour->second;
ItNode = mOpenList.find( ChildNodeIndex );
if( ItNode == mOpenList.end() )
{
ChildNode = new sNode();
ChildNode->H = mMap.GetDistance( NodeIndex, aNodeTo );
mOpenList.insert( ItNode,
std::make_pair( ChildNodeIndex, ChildNode ) );
}
else
{
ChildNode = ItNode->second;
if( NewG >= ChildNode->G )
{
continue;
}
}
ChildNode->G = NewG;
ChildNode->F = ChildNode->G + ChildNode->H;
ChildNode->Parent = NodeIndex;
}
}
Cleanup();
return false;
}
A példa programkódok az átláthatóság érdekében nem optimális módon készültek el. Jó módszer lehet a node-okat nem menet közben generálni, hanem a teljes térképre előre legenerálni őket, amennyiben a sebesség fontosabb a memóriahasználatnál, illetve ha a teljes keresési tér belefér a memóriába. Open-list-re így legalkalmasabb egy prioritási lista (priority queue) használata node indexekkel, melyben mindig a legkisebb költségű node van a gyökérben, így megspórolva a keresést a node kibontásnál. A Closed-list megszűnik és magába a node-ba kerül bele annak állapota, hogy melyik listában is található.
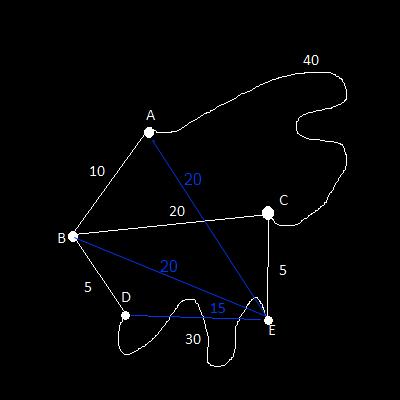
AStar Sample 1
Először is berakjuk A-t az open-list-be 0-ás G-vel és 20-as H, illetve F-fel, ahonnan egyből ki is szedjük és átrakjuk a closed-list-be. A 2 generált szomszéd, akik bekerülnek az open-list-be B és C lesznek. B 10-es G-vel, 20-as H-val, és így 30-as F-fel, míg C 40-es G-vel, 5-ös H-val és így 45-ös F-fel.
Mivel B-nek van az open node-ok között a legkisebb teljes költsége, kiszedjük onnan és átrakjuk a closed-ba. Legenerálódik D szomszéd, immár 15-ös G-vel, 15-ös H-val és így 30-as F értékkel. C már benne volt az open-listben, viszont nagyobb G költséggel, így az frissítésre kerül. Az új G-je 30 lesz, a H-ja nyilván változatlan, az F pedig 35-re módosul, illetve átállítódik a parent B-re. Szemmel is jól látható, hogy B érintésével valóban olcsóbb C-be jutni. Az A node mivel már a closed list-ben van, nem kerül kifejtésre. És mint látjuk értelme se sok volna, hiszen egy oda-vissza úttal nem érnénk el jobb eredményt, mintha nem is mozdultunk volna el A-ból.
Most D a legkisebb F értékű az open-list-ben, így E kerül be az open-list-be a kifejtsékor (B nem, mivel closed-ban van már). E pont G értéke 45 lesz, H-ja 0, mivel ez az elérni kívánt pont, F pedig ezáltal szintén 45. Azt hihetnénk, hogy kész is vagyunk, de ha megnézzük az algoritmus leírását, a cél elérésnek vizsgálata nagyon helyesen nem itt történik.
Most C pont a legkisebb F költségű az open-listben a maga 35-ös értékével. Ennek kifejtése már nem generál új szomszédokat, viszont E értékei frissítésre kerülnek, hiszen annak új G és ezáltal F értéke 35 lesz.
Az open-list-ünkben ebben a példában már csak egy elemünk maradt, ami ezáltal a legkisebb F értékű is egyben, maga az E pont, 35-ös értékkel, ami a teljes út költsége. A parenteken végig menve szépen vissza is kapjuk az útvonalat. E-be C-ből a legjobb jönni, oda B-ből, oda A-ból, vagyis a keresett útvonal: A, B, C, E.
A költséggel szembeni egyetlen kritérium, hogy ne negatív érték legyen, így az algoritmus nem kerül végtelen ciklusba azáltal, hogy 2 pont között oda-vissza ugrál, csökkentve ezzel az út költségét.
Foglalkozzunk kicsit a heurisztikával, vagyis a távolság becslő függvénnyel. Milyen kritériumoknak kell ennek megfelelnie:
- Ne becsülje túl a költséget
- Minél közelebbi becslést adjon
- Ne adjon téves becslést
Mit is jelentenek ezek. A légvonalbeli távolság azért nagyon jó becslés, mert annál biztosan hosszabb úton tudunk eljutni csak az adott pontba, feltéve, hogy nem tudunk teleportálni. Ez azért a legfontosabb és egyben elengedhetetlen kritérium, mert ha túlbecsülnék az utat, akkor az algoritmus nem tudná garantálni, hogy a legrövidebb utat találjuk meg. Példánkban ha C és E pont távolságát mondjuk 50-re becsülnénk, akkor a D pont kifejtése után nem a C, hanem az E, vagyis a végpontot szednénk ki az open-list-ből, ami azt eredményezi, hogy nem találjuk meg a legoptimálisabb útvonalat, vagyis a C-n keresztül E-be vezetőt.
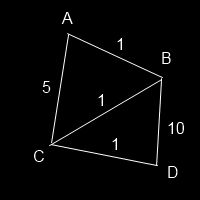
AStar Sample 2
A 2-es példában A-ból megyünk D-be, B és C ki van fejtve. C az az elem, amit az open-list-ből átraknánk a closed-ba, viszont nem jó a heurisztikánk! B-ből D-be a közvetlen út nem lehet 10, vagyis a becsült távolság, hiszen C érintésével 2 alatt elérhető volna, ezért kerülne hibásan a C node a closed-list-be, ami nem lehet, mert előbb B-t kéne kifejteni, hogy C értékei frissüljenek a rövidebb megközelíthetőség által.
A második és harmadik pontok összefüggenek. A lényeg az, hogy ha jó becslést adunk, azzal a keresést tudjuk optimalizálni. Az első példából ugyan nem látszik, de tegyük fel, hogy heurisztikának a 0-t választjuk. Ez egy “jó” heurisztika, hiszen nem becsüli túl a hátralévő utat, mégis elviheti a keresést rossz irányba, felesleges node-ok kerülhetnek kifejtésre. Például ha A pontból vezetne egy 10 pontból álló sorozat a céltól pont ellenkező irányba, melyek mindegyikének súlya 1, akkor a kereső A pont kifejtése után először ezt a 10 pontot fejtené ki, hiszen ezek összköltsége mind 10 alatt lenne, ami kisebb mint a B ponté, ami esetünkben kifejtésre került. Ez az eset egyébként egy (súlyozott) szélességi bejárásnak felel meg, hiszen A-tól mindig a legközelebbi következő pontot fejti ki, amíg E-be el nem jutunk.
Az útvonalkeresőnket használhatjuk még egyéb célokra is. Érdekes, ha mondjuk egy ponttól minél jobban el szeretnénk távolodni, ezt egyszerűen megoldhatjuk negatív távolság használatával heurisztikaként. Így az algoritmus azon node-okat fejti ki korábban, amik a célponttól minél távolabb vannak, hiszen ezek összköltsége lesz alacsonyabb. Ez esetben arra kell ügyelnünk, hogy a megállási feltételt módosítsuk, például egy adott légvonalbeli távolság elérésére.
Emellett lehetőség van lehetséges lépések generálására is az algoritmus segítségével. Az előző esethez hasonlóan ilyenkor a megállási feltétel adott távolság, vagy lépésszám elérése. Például ha azt szeretnénk tudni, hogy mely pontok érhetőek el A-ból 30 távolságon belül, akkor 0-s heurisztika használatával, megállási feltételként a 30-as távolság elérését használva, ezen pontok a close-list-be került node-ok lesznek. Mivel az összes node-nak megvan, hogy honnan juthatunk el oda, eredményül az A, B, C, D pontokat fogjuk kapni, melyekhez tartozó útvonalak az A, AB, ABC, ABD.
Az algoritmust nagy előszeretettel használják, mert viszonylag gyorsan adja vissza az optimális útvonalat, de essen azért néhány szó az eljárás hátrányairól is.
Ha nincs út a két pont között, az algoritmus az összes node-ot kifejti, ami nagy keresési térnél rengeteg ideig tart. Ez elkerülhető például egy előregenerált struktúra használatával, ami külön csoportokba gyűjti az egymásból elérhető node-okat, így egy gyors vizsgálattal eldönthető, hogy van- értelem egyáltalán a keresés elkezdésének.
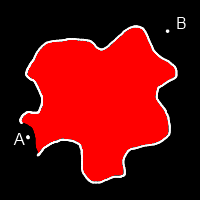
AStar Sample 3
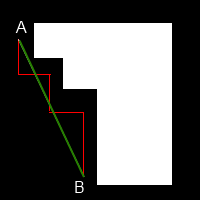
AStar Sample 4
Az algoritmus további hátránya, hogy nehezen kezeli a különböző méretű egységeket, annak implementálása tovább bonyolítja a rendszert. Itt arra kell gondolni, hogy egy gyalogos átfér egy szűk helyen, ahol egy tank például nem, illetve a falhoz is közelebb tud simulni, tehát más útvonalon közlekedik mérettől függően. A kanyarodási ívét az egységeknek már nem is említem.
Konklúzióként annyit, hogy az A* algoritmus nagyon jól működő és könnyen implementálható útvonalkereső, amely jól alkalmazható táblás, körökre osztott játékokban, és stratégiai játékokban, ahol a tile alapú mozgás megfelelő precízítású és elegendő a 2 dimenziós keresés, ám a mai komolyabb játékoknak ez már nem elegendő, ezekben a navigációs mesh-ek alkalmazása elengedhetetlen, amiről majd talán a későbbiekben írok egy újabb cikket.